Materiály ke cvičení předmětu Matematika B (B413002), VŠCHT

Podmínky zápočtu: akitvní účast na cvičení, maximálně 3 absence, na konci semestru v 11. týdnu souhranný domácí úkol (5 příkladů)

1. cvičení - lineární závislost a nezávislost vektorů, hodnost matice, násobení matic

Domácí úkol na 1.týden - Řešení úkolu

2. cvičení - determinanty, soustavy lineárních rovnice

Domácí úkol na 2.týden - Řešení úkolu

3. cvičení - inverzní matice, vlastní čísla a vlastní vektory

Domácí úkol na 3.týden - Řešení úkolu

4. cvičení - geometrie v R3 (vzájemná poloha rovin), vlastnosti množin v R2

Domácí úkol na 4.týden - Řešení úkolu

5. cvičení - funkce více proměnných, parciální derivace

Domácí úkol na 5.týden- Řešení úkolu

6. cvičení - funkce více proměnných, řetízkové pravidlo, tečná rovina a totální diferenciál

Domácí úkol na 6.týden - Řešení úkolu

7. cvičení - funkce více proměnných - Taylorův polynom, Newtonova metoda, hledání lokálních extrémů

Domácí úkol na 7.týden - Řešení úkolu

8. cvičení - věta o implicitních funkcích, metoda nejmenších čtverců

Domácí úkol na 8.týden - Řešení úkolu

9. cvičení - křivkové integrály

Domácí úkol na 9.týden - Řešení úkolu

10. cvičení - potenciální vektorové pole

Domácí úkol na 10.týden - Řešení úkolu

11. cvičení - dvojný integrál - Fubiniova věta

Domácí úkol na 11.týden - Řešení úkolu

12. cvičení - dvojný integrál - substituce do polárních souřadnic, soustavy lineárních diferenciálních rovnic 1. řádu

Domácí úkol na 12.týden

 

Zadání souhrnného domácího úkolu - termín odevzdání do neděle 23.5. 23:59

 

Odkaz na e-learning - materiály a výuková videa k předmětu Matematika B

Archiv k předmětu Matematika A

Doplňující obrázky a videa

Video - vrstevnice funkce dvou proměnných a aplikace věty o implicitních funkcích

Video - graf funkce dvou proměnných f(x,y)=sqrt(y-x^2) a jeho řezy

Video - vlastnosti množin v R^2

 

Dodatek k 5. cvičení (vrstevnice) - vrstevnice vzniklá řezem grafu funkce f(x,y)=sqrt(y-x^2) rovinou z=2

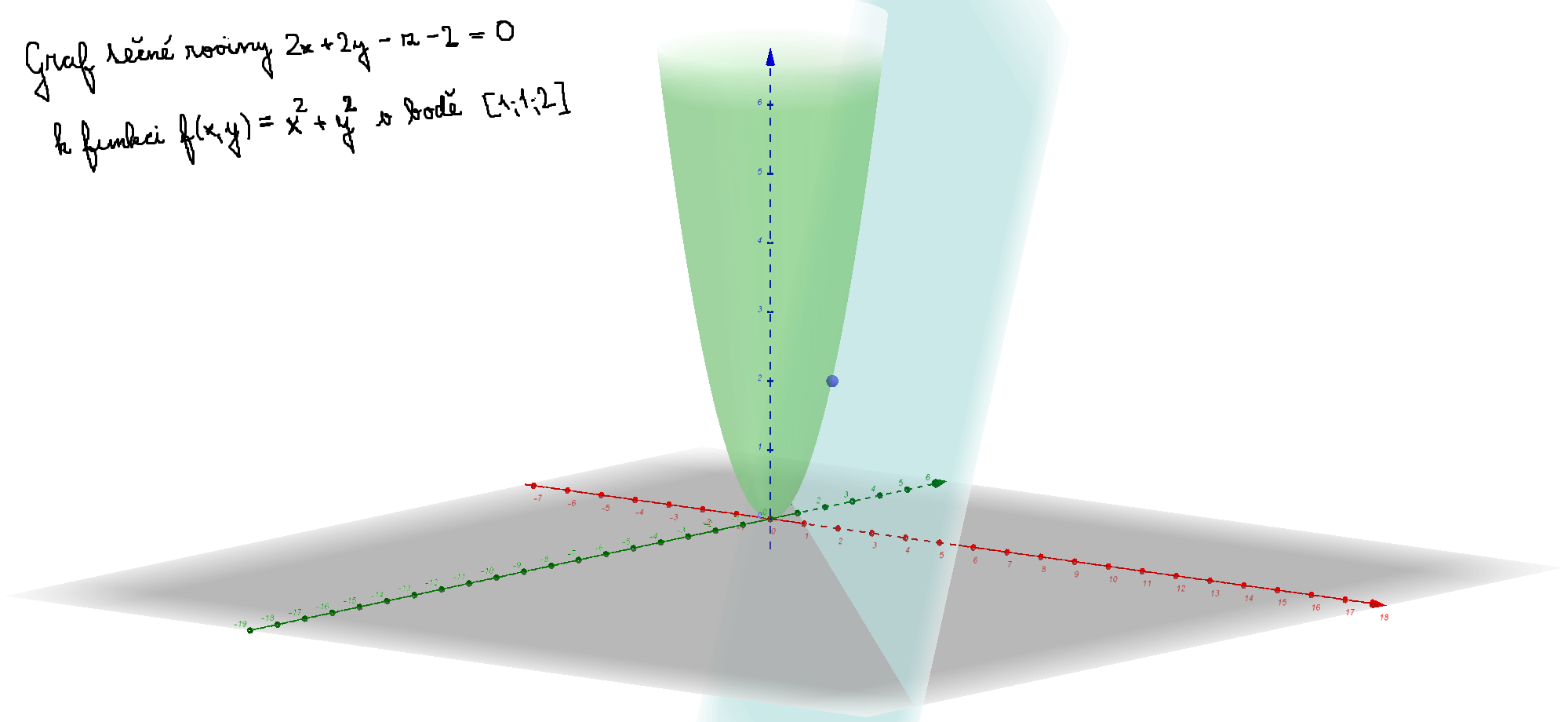
Dodatek k 6. cvičení (tečná rovina) - tečná rovina ke grafu funkce f(x,y)=x^2 + y*2 v bodě [1;1]

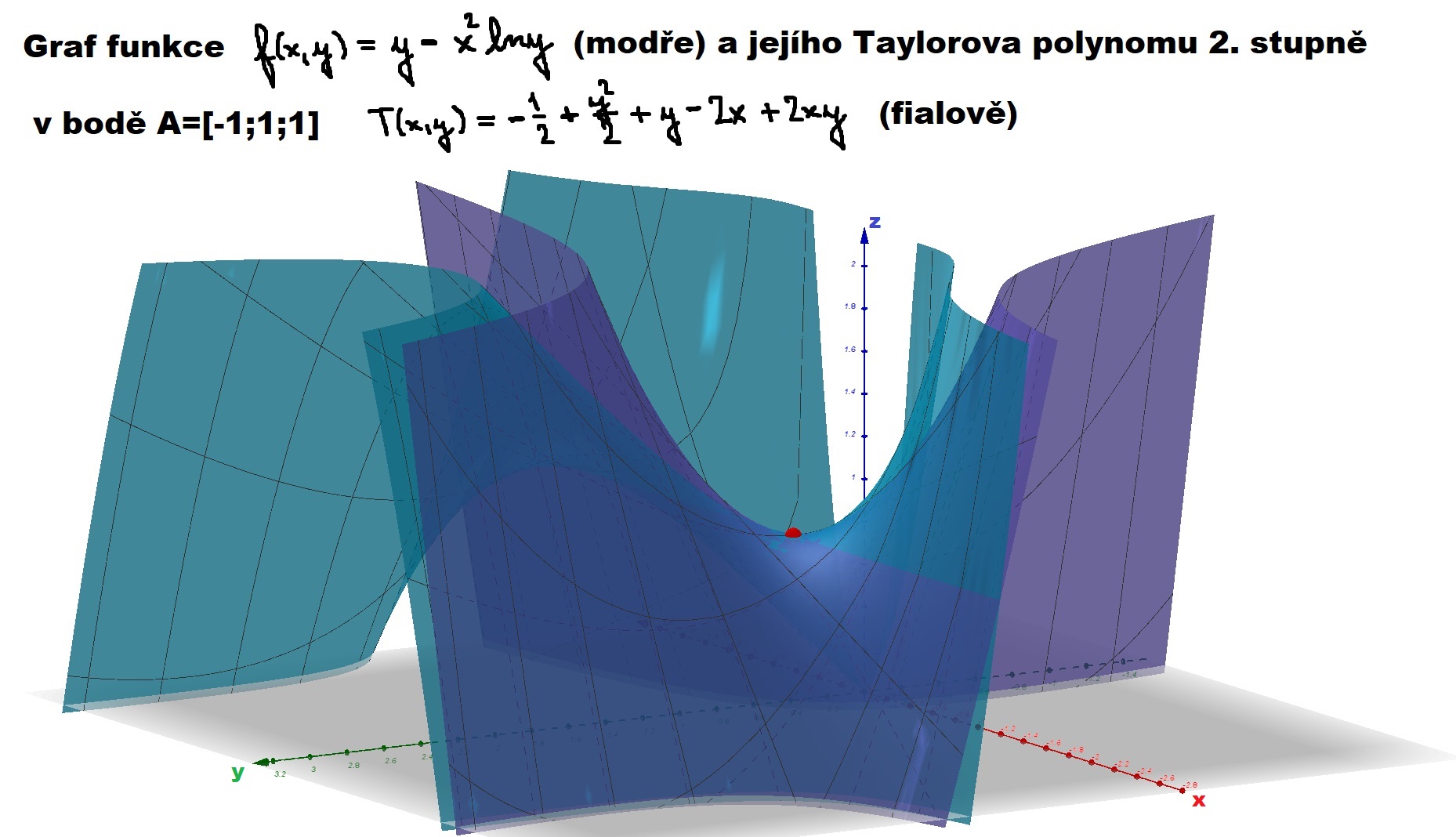
Dodatek k 7. cvičení (DÚ 1.příklad) - graf funkce f(x,y)=y - x^2 ln(y) a jejího Taylorova polynomu v bodě A=[-1,1,1]

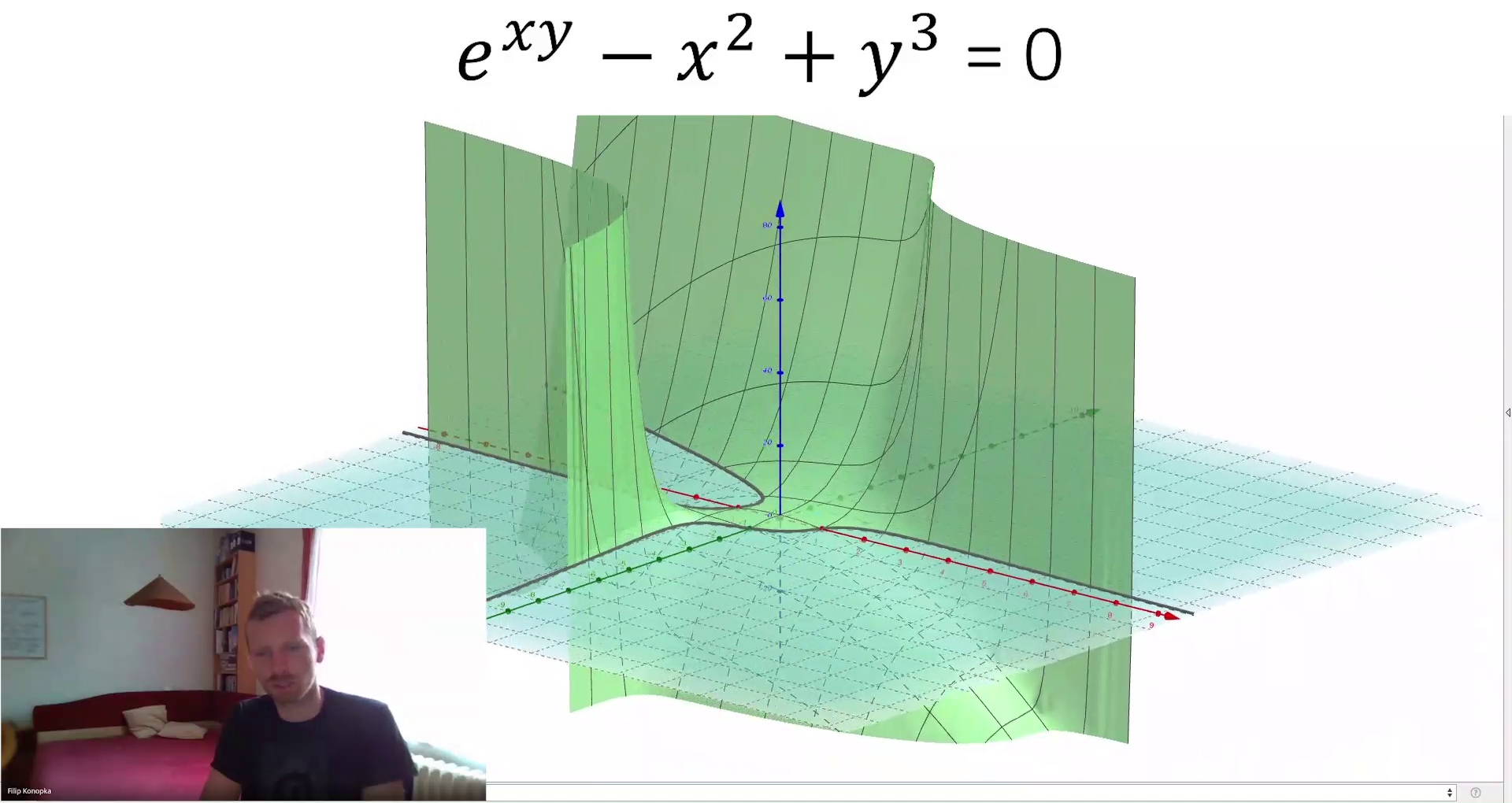
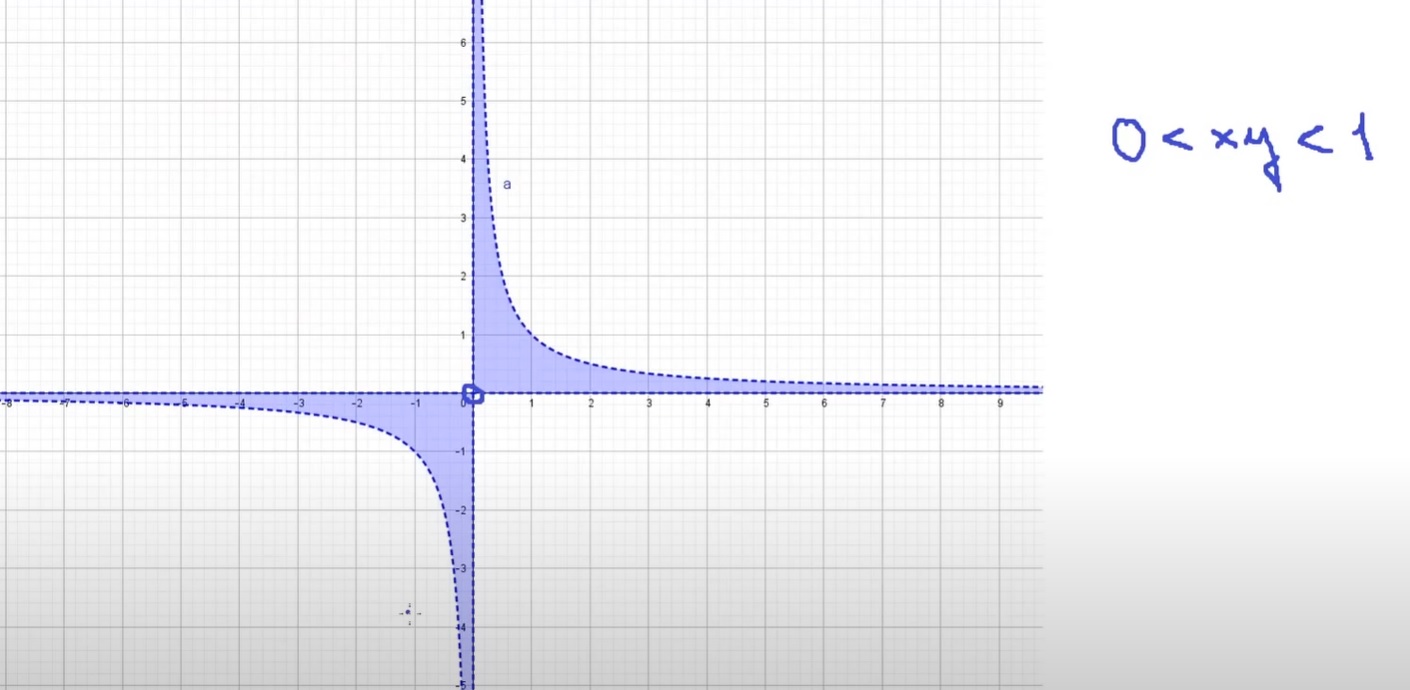
Dodatek k 8. cvičení (VOIF) - křivka daná rovnicí cos(x)/y=1-xy a Taylorovy polynomy v bodě [0;1]

 

Doporučený postup při studiu každého tématu:

1) Aktivně zhlédnout (tedy s porozuměním) video přednášky k danému tématu. Případné nejasnosti v teorii konzultovat se skripty, event. s přednášejícím. 

2) Aktivně zhlédnout (nejprve zkusit příklady vyřešit samostatně) video s řešenými příklady. Případné nejasnosti konzultovat se sbírkou, event. se cvičícím. 

3) Projít si v e-learningu místo cvičení příslušnou prezentaci. Neřešené příklady vyřešit. Případné nejasnosti v příkladech konzultovat se cvičícím (online konzultace).

4) Aktivně se zúčastnit  online cvičení/konzultace se svým cvičícím, připravit si konkrétní dotazy, pokud máte v látce nějaké nejasnosti.

5) Pokračovat v procvičování na příkladech ze sbírky.

6) Vypracovat dobrovolný domácí úkol. 

 

 

 

Sylabus předmětu

1. Vektory a matice, maticová algebra, skalární součin. Lineární nezávislost vektorů a hodnost matice.

2. Soustavy lineárních algebraických rovnic. Determinant matice, vektorový součin.

3. Inverzní matice. Vlastní čísla matic. Geometrie v rovině a v prostoru.

4. Euklidovský prostor, metrika, norma, vlastnosti podmnožin.

5. Funkce více reálných proměnných. Parciální derivace, parciální derivace složených funkcí. Směrová derivace, gradient. Totální diferenciál, tečná rovina.

6. Taylorův polynom funkcí 2 proměnných. Newtonova metoda pro soustavu 2 nelineárních rovnic o 2 neznámých.

7. Extrémy funkcí dvou proměnných. Metoda nejmenších čtverců.

8. Implicitně zadané funkce jedné a více proměnných a jejich derivace.

9. Křivky dané parametricky, tečný vektor ke křivce, hladká křivka, orientace a součet křivek.

10. Vektorová pole v rovině a v prostoru. Křivkový integrál vektorového pole a jeho fyzikální význam.

11. Nezávislost křivkového integrálu na integrační cestě. Potenciál vektorového pole. Diferenciální formy a jejich integrace.

12. Dvojný integrál a jeho geometrický význam. Výpočet dvojného integrálu postupnou integrací - Fubiniova věta.

13. Substituce pro dvojný integrál. Polární souřadnice. Laplaceův integrál.

14. Soustavy dvou diferenciálních rovnic 1. řádu. Řešení autonomních soustav lineárních diferenciálních rovnic s konstantními koeficienty. Model "Dravec-kořist".

Sbírky úloh a studijní texty